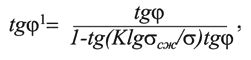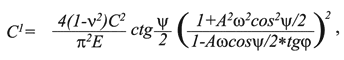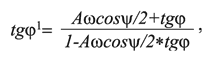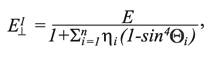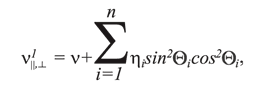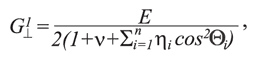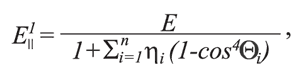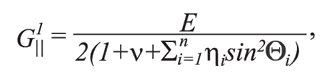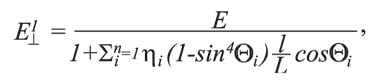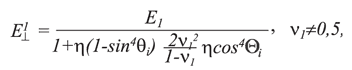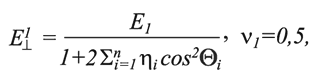Маркшейдерия и недропользование

Метод исследования геомеханического состояния прибортового массива, подработанного подземными горными выработками, должен удовлетворять следующим требованиям:

охватывать в рассмотрении значительную часть горного массива, включающую борт, часть дна карьера, подземные пустоты и расположенные в них поддерживающие целики;

обеспечивать оперативность получения результатов исследования;

позволять прогнозировать геомеханическое состояние массива в изменившихся вследствие выполнения горных работ геотехнических условиях.

Перечисленным требованиям наиболее полно удовлетворяет комплексный метод теоретического исследования, базирующийся на надежных результатах экспериментального изучения физико-механических свойств пород, слагающих прибортовую зону карьера.

Теоретический подход к задаче исследования предполагает наличие определенной геомеханической модели породного массива. Для различных типов пород, находящихся в различных условиях нагружения, в настоящее время известно большое число моделей, наиболее известными из которых являются следующие: упругая модель Гука (рис.1а), вязкоуп-ругие модели Кельвина-Фойгта (рис.1б), Гогенемзера-Прагера (рис.1в), Пойнтинга-Томпсона (рис.1г), жесткопластическая модель (рис.1д), упругопластическая модель (рис.1е), вязкоупругопластические модели Шведова-Бингама (рис.1ж) и схема с последовательным соединением элементов (рис.1з), упругопластическая неоднородная модель, учитывающая частичное разрушение породы; раздельно-блочная модель, в которой породный массив представляется сложенным из отдельных структурных блоков.

Следует отметить, что все модели, схемы которых представлены на рис.1б-1з, характеризуются наличием вязкого или жесткопластического элементов.

Экспериментальные исследования механических свойств скальных пород, выполненные А.Н. Ставрогиным [1], показывают, что пластическое состояние пород наступает при напряжениях в них, измеряемых десятками и сотнями МПа. Такие напряжения характерны для больших глубин залегания пород (600 и более метров), поэтому при расчетах устойчивости бортов карьеров глубиной до 200-300 метров учитывать возможность перехода пород в пластическое состояние нецелесообразно.

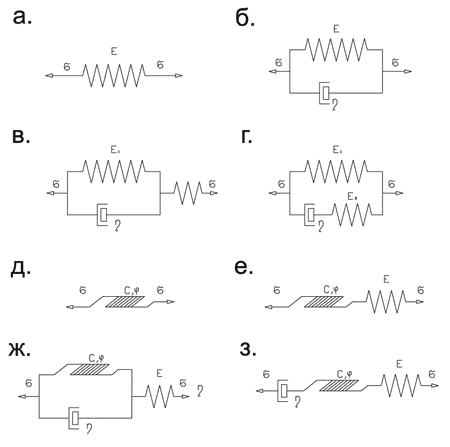Рис. 2.
Основные модели идеальных сред: а – схема упругой модели Гука; б – схема вязкоупругой модели Кельвина-Фойгта; в – схема вязкоупругой модели Гогенемзера-Прагера; г – схема вязкоупругой модели Пойнтинга-Томпсона; д – схема жесткопластической модели; е – схема упругопластической модели; ж –схема вязкоупругопластической модели Шведова-Бингама; з – схема вязкоупругопластической модели с последовательным соединением элементов.

Для моделей с жесткопластическим элементом (рис.1д-1з) исходными данными для расчетов являются сцепление (С, МПа) и угол внутреннего трения пород (ρ, градус). Для скальных трещиноватых пород относительно механизма формирования значений этих показателей и о самих значениях в настоящее время существуют весьма противоречивые суждения. Это связано с тем, что механические свойства пород, определенные в образце, существенно отличаются от таковых в массиве. Поэтому для переноса результатов лабораторных испытаний образцов на натурные условия обычно используют переходные коэффициенты, так называемые коэффициенты структурного ослабления, численные значения которых, в зависимости от характера нарушенности породного массива, определяются по различным методам, методикам, формулам и зависимостям. Однако, анализ наиболее известных методов, методик и зависимостей, приведенный в работе [2], показывает, что в некоторых конкретных случаях результаты расчетов по различным методам отличаются друг от друга более чем на 300%. Поэтому совершенно справедливым представляется сделанный в той же работе [2] вывод о том, что надежную оценку прочности структурно-нарушенных массивов, а в нашем случае получение надежных исходных данных для расчетов, можно осуществить, только зная «истинные» значения прочности по поверхностям ослабления (контакты пород, наслоения, трещины и т.д.), разбивающим эти массивы.

Для определения значений сцепления C¹ и угла внутреннего трения φ´ в породах с раскрытой трещиной Н. Бартоном и В. Чубеем [3] предложены следующие зависимости:

(1)

(2)

где σ - действующее нормальное напряжение, МПа; σ_сж – предел прочности при одноосном сжатии пород в образце, МПа; К - коэффициент, характеризующий шероховатость контакта и численно равный среднему углу наклона шероховатостей; С и С¹ - соответственно значения сцепления пород в образце и в массиве, МПа; φ и φ´ - соответственно значения угла внутреннего трения пород в образце и в массиве, градус.

Сотрудниками лаборатории горной геомеханики института «Гипроцветмет» [4] для определения этих же показателей предложены иные зависимости, а именно:

(3)

(4)

где А – амплитуда волнистости трещины, м; ω – круговая частота волнистости, м^-1; ν – коэффициент Пуассона; Е – модуль Юнга породы, МПа; ψ – угол смещения берегов трещины, с; С – сцепление, обусловленное микрошероховатостью трещины, МПа; π = 3,14.

Описанная ситуация обуславливает определенный произвол в выборе надежных значений прочностных характеристик (сцепление, С¹ и угол внутреннего трения, φ´ пород в массиве. Положение усугубляется еще и тем, что, как правило, реальный горный массив сложен различными породами, расчлененными различными системами трещин. Так, например, в районе Центрального рудного поля Жезказганского месторождения выделяется 4 основных типа пород, разбитых 5 главенствующими системами трещин. Очевидно, что в данном конкретном случае детальное изучение параметров шероховатости контактов трещин не представляется возможным.

Как уже отмечалось выше, для бортов карьеров высотой 200-300 м максимальные напряжения в прибортовой зоне обычно не превышают 5-8 МПа. В этом диапазоне напряжений для большинства скальных и полускальных пород характерна линейная зависимость относительной деформации от действующего напряжения. Этот факт позволяет рассматривать геомеханическое состояние горного массива в прибортовой зоне в рамках линейной теории упругости, основными исходными данными в которой являются плотность – γ, коэффициент Пуассона – ν и модуль Юнга – E породы.

Определение плотности пород, как правило, не вызывает затруднений. Коэффициент Пуассона легко может быть определен для образцов с различной ориентацией закрытых трещин на установке, разработанной в лаборатории горной геомеханики института «Гипроцветмет» [4]. Для определения модуля Юнга в натурных условиях существует целый ряд приборов и устройств, таких как передвижной штамп конструкции Ленгидропроекта, давильная установка конструкции ВНИМИ, прессиометры различных конструкций. Определение модуля Юнга в лабораторных условиях также не представляет трудностей.

С учетом изложенного выше и результатов исследований К.В. Руппенейта, приведенных в работе [5], значения модуля Юнга Е¹, коэффициента Пуассона ν´ и модуля сдвига G для породных массивов с различными характеристиками трещиноватости могут быть определены из следующих выражений:

1. Длина трещины больше размера исследуемой области. Число различно ориентированных систем трещин – от одной до трех.

(5)

(6)

(7)

где E_⊥¹ – значение модуля Юнга в породном массиве в направлении, перпендикулярном оси Х, МПа; Е – значение модуля Юнга в образце, МПа; Θ_i – угол между направлением трещины i-ой системы и осью Х, градус; η – число систем трещин, шт;

δ_i – ширина раскрытия i-ой трещины, м; β_i = 3 х 10^-4 – среднестатистическая относительная площадь скальных контактов [5]; h_i - среднее расстояние между двумя трещинами i-ой системы, м; ν_||,⊥² – значение коэффициента Пуассона в породном массиве в направлении, параллельном и перпендикулярном оси Х; G_||,⊥² - значение модуля сдвига в направлении перпендикулярном оси Х, МПа.

(8)

(9)

где E_||¹ – значение модуля Юнга в породном массиве в направлении, параллельном оси Х, МПа;G_||¹ – значение модуля сдвига в направлении параллельном оси Х, МПа.

2. Хаотичное расположение трещин. Мощность образуемых расслоений примерно одинакова. Массив рассматривается как квазиизотропный.

Модуль Юнга Е¹ определяется по формуле (5) или по упрощенной формуле (3).

(10)

3.Породный массив, эквивалентный сыпучей среде.

(11)

где К – коэффициент пустотности (отношение объема трещин к объему породы).

4. Система выклинивающихся трещин. Длина трещин меньше размеров исследуемой области L.

(12)

5. Трещины с заполнителем.

(13)

(14)

где

Е₁ и ν₁ – соответственно значения модуля Юнга и коэффициента Пуассона материала заполнителя трещин, МПа.

Таким образом, по формулам (5-14) можно рассчитать значения исходных данных практически для всех имеющих место производственных ситуаций.

Выводы

- для исследования геомеханического состояния прибортового массива карьера, подработанного подземными горными выработками, наиболее целесообразным является теоретический метод;

- наиболее приемлемой с точки зрения достоверности результатов исследований является линейно упругая модель горного массива.