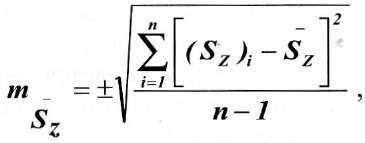 В результате исследования погрешностей расчета типовых распределений оседаний земной поверхности над горными выработками угольных шахт установлено, что в полумульде сдвижения находится характерная (особая) точка - точка максимального варьирования ординат единичных кривых оседания. Математическое моделирование влияния погрешности определения граничной точки сдвижения на распределение единичных кривых показывает, что особая точка смещена от точки перегиба в сторону граничной зоны сдвижения примерно на 0,1 длины полумульды. Характерная точка - это виртуальная точка и ее появление объясняется процессом трансформирования кривых оседания в единичные и типовые кривые.
В результате исследования погрешностей расчета типовых распределений оседаний земной поверхности над горными выработками угольных шахт установлено, что в полумульде сдвижения находится характерная (особая) точка - точка максимального варьирования ординат единичных кривых оседания. Математическое моделирование влияния погрешности определения граничной точки сдвижения на распределение единичных кривых показывает, что особая точка смещена от точки перегиба в сторону граничной зоны сдвижения примерно на 0,1 длины полумульды. Характерная точка - это виртуальная точка и ее появление объясняется процессом трансформирования кривых оседания в единичные и типовые кривые.
Методика трансформирования кривых оседания земной поверхности в единичные и типовые кривые
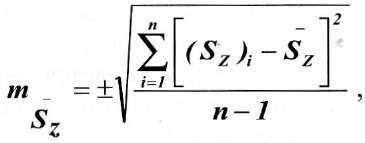 В результате исследования погрешностей расчета типовых распределений оседаний земной поверхности над горными выработками угольных шахт установлено, что в полумульде сдвижения находится характерная (особая) точка - точка максимального варьирования ординат единичных кривых оседания. Математическое моделирование влияния погрешности определения граничной точки сдвижения на распределение единичных кривых показывает, что особая точка смещена от точки перегиба в сторону граничной зоны сдвижения примерно на 0,1 длины полумульды. Характерная точка - это виртуальная точка и ее появление объясняется процессом трансформирования кривых оседания в единичные и типовые кривые.
В результате исследования погрешностей расчета типовых распределений оседаний земной поверхности над горными выработками угольных шахт установлено, что в полумульде сдвижения находится характерная (особая) точка - точка максимального варьирования ординат единичных кривых оседания. Математическое моделирование влияния погрешности определения граничной точки сдвижения на распределение единичных кривых показывает, что особая точка смещена от точки перегиба в сторону граничной зоны сдвижения примерно на 0,1 длины полумульды. Характерная точка - это виртуальная точка и ее появление объясняется процессом трансформирования кривых оседания в единичные и типовые кривые.
Характерная точка позволяет расчетным путем выходить на границу мульды сдвижения. При этом ординаты типовых распределений оседаний определяются в 2-3 раза точнее по сравнению с типовыми распределениями, получаемыми по традиционному подходу с применением граничных критериев процесса сдвижения.
The method of transforming the curves of earth surface subsidence into single and typical curves
Using the new geometry element of displacement trough in mining practice allows calculating the parameters of displacement process with a considerably greater accuracy than with the use of the generally accepted technique
Кроме того, граничные углы, рассчитанные с применением координат особой точки, характеризуются меньшей погрешностью по сравнению с граничными углами, полученными с использованием в настоящее время граничных критериев.
Предлагаемая нами методика трансформирования кривых оседания в единичные и типовые кривые заключается в следующем [1].
-
Кривые оседания земной поверхности в полумульдах сдвижения ограничиваются точкой максимального оседания и граничной точкой сдвижения.
- Местоположение и величина максимального оседания могут быть установлены при помощи полинома третьей степени, который адекватно отражает распределение оседаний в окрестности точки с наибольшим измеренным оседанием. Путем исследования полинома третьей степени на максимум находятся величина и местоположение точки максимального оседания. Такой подход основывается на том, что не всегда репер, получивший наибольшее оседание, является точкой максимального оседания.
- Граничная точка мульды сдвижения определяется по известным граничным критериям: оседание 15 мм, наклон 0,5 · 10-3 , деформация растяжения 0,5 · 10-3.
-
Кривая оседания трансформируется в единичную кривую. Длина полумульды сдвижения принимается за единицу. Реперы профильной линии координируются, т. е. их относительные абсциссы вычисляются по формуле:
z = x / L , (1) - где: х - расстояние от точки максимального оседания до репера;
- L - длина полумульды сдвижения.
В каждой точке z вычисляются относительные оседания по формуле:
Sz = ηx / ηm , (2) - где: ηx - оседание репера в точке с абсциссой х;
- ηm - максимальное оседание земной поверхности.
-
Единичная кривая оседания сглаживается методом ступенчатой аппроксимации путем применения функции Гаусса в виде
Sz = e -a z² . (3) По актическим величинам Sz и z вычисляется коэффициент по формуле:
α = - ln Sz / z² . (4) По методу наименьших квадратов устанавливается зависимость: α=f (z), тогда выражение для единичной кривой приобретает следующий вид:
Sz = e -f (z) z² (5) - Единичная кривая задается таблично через 0,1 полумульды сдвижения путем вычисления ординат Sz в точках z.
-
Единичные кривые усредняются, т.е. в каждой точке деления полумульды находится среднее значение ординаты
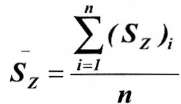
(6) где n - исло полумульд сдвижения.
-
Вычисляются средние квадратические погрешности ординат типовой кривой оседания
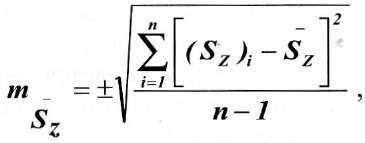
(7) и по оси z строится распределение этих погрешностей.
- Устанавливаются координаты характерной точки полумульды: абсцисса zm находится по местоположению максимальной величины погрешности mSz , а ордината Szm вычисляется как среднее арифметическое из ординат единичных кривых в точке zm.
-
Каждая единичная кривая обрабатывается в такой последовательности :
- на относительной ординате максимального оседания откладывается величина Szm и параллельно оси z проводится линия до пересечения с единичной кривой;
- определяется абсцисса z точки встречи кривой с проведенной линией;
-
вычисляется расчетная длина полумульды сдвижения
L = Z / Zm ; - длина L откладывается от точки максимального оседания и таким образом находится расчетная граничная точка.
- Методом ступенчатой аппроксимации устанавливается аналитическое выражение каждой единичной кривой, которая задается таблично через 0,1 длины полумульды сдвижения.
-
Полученные единичные кривые усредняются и выводится типовая кривая.
Следует заметить, что оседание в точке z = 1,0 типовой кривой не равно нулевому значению, поэтому следует путем экстраполяции определить местоположение нулевого оседания.
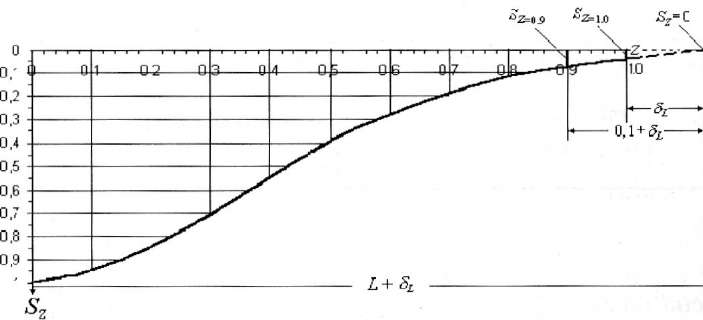
Наше предположение заключается в том, что уменьшение оседания на интервале 0,9 - 1,0 типовой кривой происходит по прямой линии и эта линия при ее продолжении пересекает линию земной поверхности в точке с ожидаемым нулевым оседанием (см. рис. 1).
Вычислим расстояние от точки z = 1,0 до точки с ожидаемым нулевым оседанием. Из подобия треугольников на граничном участке мульды следует, что
В результате преобразований получим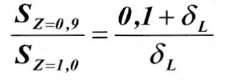
(8)
Таким образом, граничная точка будет находиться от точки максимального оседания на расстоянии L + δL.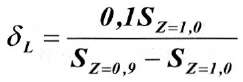
(9) - На каждой единичной кривой оседания определяется граничная точка с ожидаемым нулевым оседанием путем увеличения длины полумульды на δL .
- Устанавливается аналитическое выражение каждой единичной кривой по методу ступенчатой аппроксимации, а затем рассчитываются значения ординат в точках деления полумульд.
- Ординаты единичных кривых усредняются и, таким образом, выводится типовая кривая оседания с граничным нулевым оседанием.
Типовая кривая, рассчитанная по предлагаемой нами методике, характеризуется меньшей величиной погрешности по сравнению с типовой кривой, полученной традиционным способом. Уменьшение максимальной величины погрешности происходит в 2 - 3 раза. Рис. 2 иллюстрирует пример такого сравнения.
Сравним граничные углы сдвижения, полученные по деформации растяжения и граничные углы, рассчитанные с использованием характерной точки мульды сдвижения.
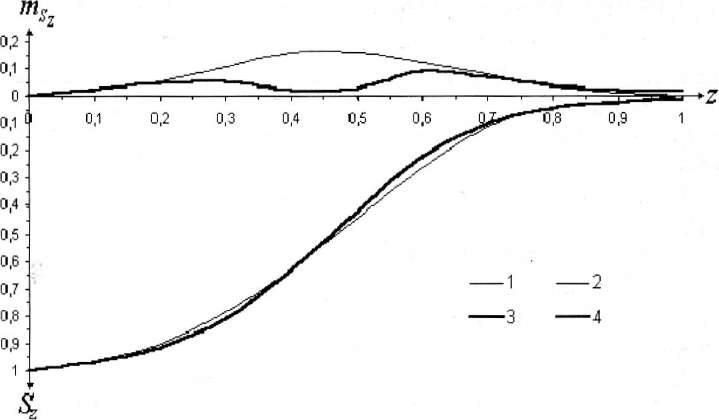 Рис. 2.
Рис. 2.Типовые кривые оседания и их погрешности: 1- кривая, полученная по граничному критерию; 2 - погрешность ординат кривой 1; 3 - кривая, вычисленная по координатам особой точки; 4 - погрешность ординат кривой 3.
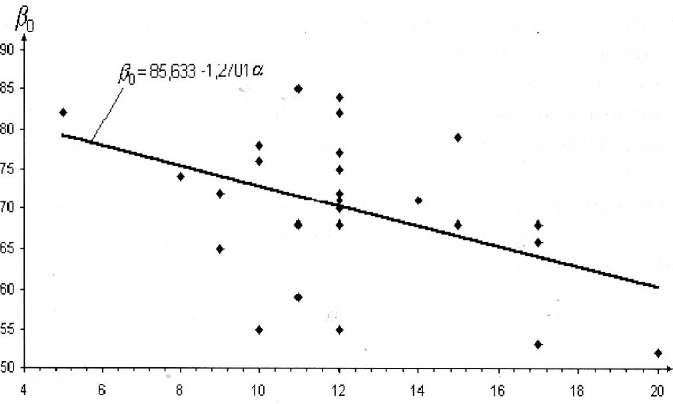
На рис. 3 показано распределение граничных углов β0, полученных по критерию растяжения 0,5 · 10-3.
Линия тренда имеет следующее аналитическое выражение: β0 = 85,6 - 1,3α , т. е. граничный угол по падению угольного пласта уменьшается с увеличением угла падения пласта по прямолинейной зависимости.
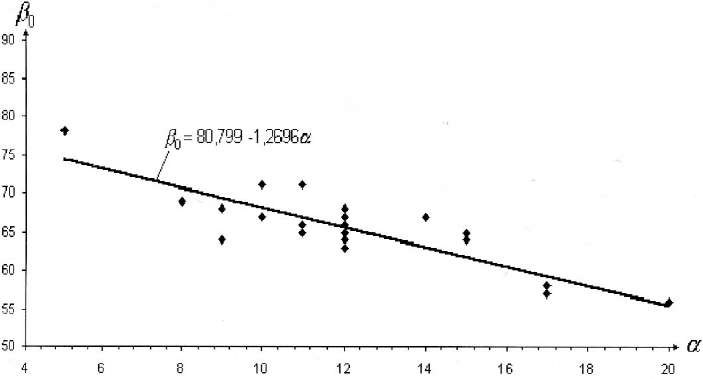
На рис. 4 представлены граничные углы, рассчитанные с применением характерной точки мульды. В результате получена такая статистическая зависимость: β0 = 80,8 — 1,3α .
Аналитическая зависимость на рис. 3 характеризуется коэффициентом достоверности аппроксимации, равном R2 = 0,1867 , а зависимость на рис. 4 — R2 = 0,7476. Теснота связи увеличилась в 4 раза при одинаковой тенденции уменьшения граничных углов с увеличением угла падения пласта. Сумма квадратов отклонений между фактическими величинами и рассчитанными по аналитическим формулам в примере традиционного подхода к определению граничных углов составляет 1813,7, а по предлагаемому нами методу - 140,5.
Наблюдается уменьшение суммы квадратов отклонений в 12,9 раза.
Средние квадратические отклонения составляют соответственно ±8,0° и ±2,2°.
Сравнение граничных углов β0, полученных по граничному критерию деформации растяжения 0,5 · 10-3, с граничными углами, рассчитанными по формулам правил охраны сооружений 1972 года, характеризуется средней квадратической погрешностью mβ0 = ±10,40.
Сравнение углов, полученных по критерию ε = 0,5 · 10-3, с рассчитанными углами по формулам правил охраны 1981 года указывает на величину mβ0 = ±10,50.
На рис. 3 при угле падения пласта α = 12° максимальное и минимальное значения граничных углов составляют, соответственно, 84° и 55°, следовательно, размах варьирования этих углов составляет 29°.
На рис. 4 при том же угле падения максимальное значение граничного угла равно 68°, а минимальное - 63°. Наблюдается уменьшение размаха варьирования граничных углов в 5,8 раза.
Таким образом, определение граничной точки сдвижения посредством нового геометрического элемента - точки максимального варьирования ординат единичных кривых оседания сопровождается значительным уменьшением погрешности определения граничных углов со стороны падения угольного пласта.
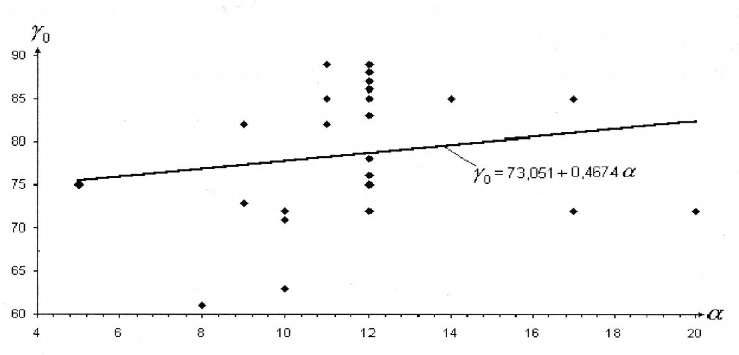
Покажем на рис. 5 распределение граничных углов γ0, полученных по критерию растяжения 0,5 · 103, в зависимости от угла падения пласта.
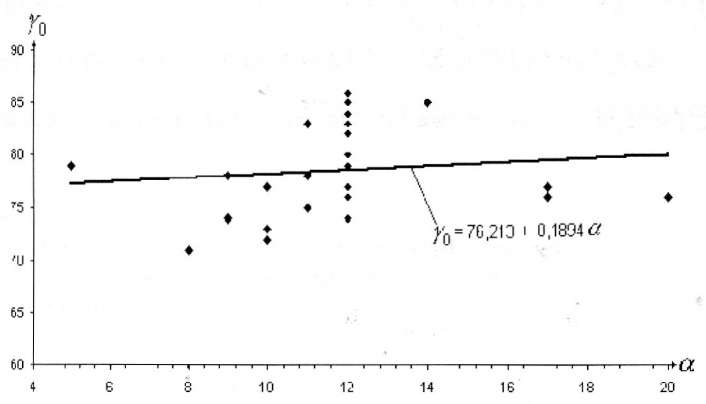
На рис. 6 приведем зависимость от угла падения пласта граничных углов γ0, полученных с применением особой точки мульды.
Сумма квадратов отклонений расчетных величин, найденных по формуле γ0 = 73° + 0,5α, от фактических, полученных по критерию граничной деформации составляет 1583,8, а средняя квадратическая погрешность mγ0 = ±7,8°.
Сумма квадратов отклонений граничных углов, рассчитанных по формуле γ0 = 76,2 + 0,2α , от граничных углов, полученных с применением особой точки, составляет 440,9. Средняя квадратическая погрешность mγ0 = ±4,1°.
Таким образом, по граничным углам сдвижения со стороны восстания угольного пласта наблюдается уменьшение суммы квадратов отклонений в 3,6 раза, а среднее квадрати- ческое отклонение уменьшилось в 1,9 раза.
Анализ показывает, что предложенный нами метод расчета граничных углов с применением особой точки мульды позволяет получать более тесные статистические зависимости.
Правила охраны сооружений 1998 г. рекомендуют в аналитических расчетах сдвижений и деформаций земной поверхности над горными выработками угольных шахт применять типовые кривые, которые находятся в зависимости от коэффициента подработанности [3].
При этом коэффициенты подработанности: n - по правилам охраны 1972 года и N - по правилам охраны 1998 года, связаны зависимостью
|
|
(10) |
Типовые кривые правил охраны 1998 г. заданы функциями Гаусса в таком виде:
|
|
(11) |
где Ф (t0), Ф (t), Ф (u) - интегралы Гаусса;
|
|
(12) |
|
|
(13) |
D - длина горной выработки; d - расстояние на плане от границы выработки до точки перегиба кривой оседания при полной подработке; С - определяемый по данным наблюдений постоянный коэффициент (в условиях Донбасса 0,2); Н - глубина горных работ; х - абсцисса точки с началом координат в точке максимального оседания.
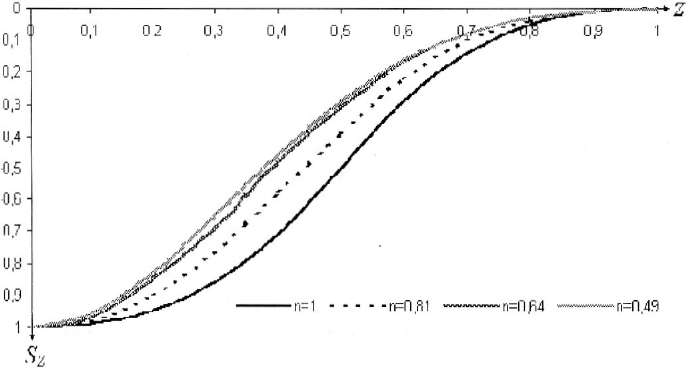
Типовые кривые правил охраны представлены на рис. 7, на котором видно, что форма типовой кривой закономерно изменяется при изменении коэффициента подработанности. Так, в точке z = 0,4 с увеличением коэффициента подработанности от 1 до 0,49 ордината типовой кривой изменяется от 0,71 до 0,46, т. е. размах варьирования составляет 0,25.
На рис. 8 приведенные типовые распределения оседаний получены поданным инструментальных наблюдений на шахтах ОАО Гуковуголь при использовании граничных критериев процесса сдвижения и координат характерной точки мульды сдвижения [4].
Видно, что в точке z = 0,4 ординаты типовых кривых изменяются от 0,58 до 0,48. Размах варьирования составляет 0,10, что в 2,5 раза меньше по сравнению с размахом ординат типовых кривых правил охрани в этой точке. При этом нет закономерного изменения величины ординаты при изменении коэффициента подработанности от 1 до 0,4.
Таким образом, кривые на рис. 8 не подчиняются основному квалификационному признаку - коэффициенту подработанности. Это позволяет выдвинуть предложение о возможности использования в практике маркшейдерских работ единой типовой кривой оседания.
На основании полученных результатов применения нового геометрического элемента мульды сдвижения - характерной точки, т. е. точки максимального варьирования ординат единичных кривых оседания, можно заключить, что предлагаемая нами методика обработки данных инструментальных измерений смещений реперов земной поверхности над горными выработками угольных шахт позволяет на новом качественном уровне рассчитывать параметры процесса сдвижения, при этом новые параметры определяются значительно точнее по сравнению с параметрами, полученными традиционным способом.
Литература
- Посыльный Ю. В. Руководство по расчету параметров процесса сдвижения земной поверхности над горными выработками, Шахт. ин-т. Новочеркасск: ЮРГТУ, 2000. -163 с. - ISBN 5 - 88998 - 126 - 9.
- Озеров И. Ф.Разработка методов расчета деформаций земной поверхности и охраны зданий при подземной добыче антрацитов Донбасса: Дис... канд. техн. наук: 05.15.01.. М., 1982. - 241с.
- Правила охраны сооружений и природных объектов от вредного влияния подземных горных разработок на угольных месторождениях, СПб., 1998. - 291 с.
- Озеров И. Ф.. Методика расчета деформаций земной поверхности и прогнозирования повреждений зданий для выбора рациональных мер их охраны при подземной добыче антрацитов Донбасса.. МУП СССР. - Гуково, 1982. - 23 с..
Меню
Календарь выставок и форумов
Уралэкспокамень 2024
Tech Mining Казахстан 2024
Сахапромэкспо-2024
Выставки и форумы одной строкой
Котировки ЦБ
| Курсы валют ЦБ РФ | с 23.11.2024 | |
|
Белорусский рубль
|
29.93 ▲(+0.45) | |
|
Доллар США
|
102.58 ▲(+1.90) | |
|
Евро
|
107.43 ▲(+1.35) | |
|
100 Казахстанских тенге
|
20.73 ▲(+0.40) | |
|
Канадский доллар
|
73.48 ▲(+1.53) | |
|
Китайский юань
|
13.94 ▲(+0.06) | |
|
10 Украинских гривен
|
24.85 ▲(+0.44) | |
| Обновление: 2024-11-23 11:22:07 | ||