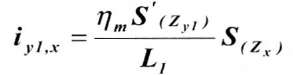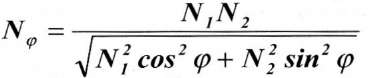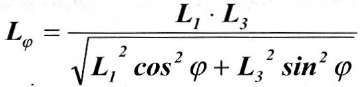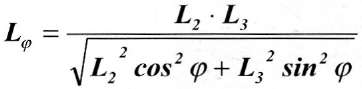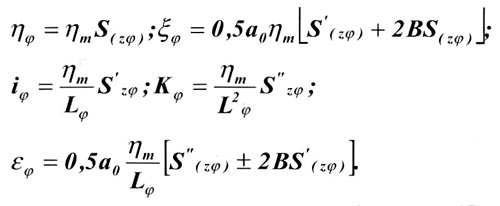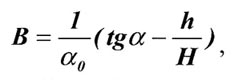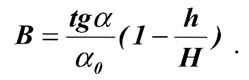
В современных условиях Донбасса, характеризующихся большими глубинами горных работ, на земной поверхности обычно образуются мульды сдвижения без плоского дна, состоящие целиком из краевых частей, в пределах которых сдвижения и деформации земной поверхности направлены под углом к простиранию и падению, а границы мульды имеют криволинейный вид. В связи с этим возникают некоторые новые рекомендации по расчету сдвижений и деформаций на краях мульды. В действующих Правилах охраны сооружений [1] метод таких расчетов предлагается. Назовем его координатным методом.
Согласно ему в любой точке на краевом участке мульды определяются сдвижения и деформации по двум взаимно перпендикулярным направлениям, параллельным координатным осям, в качестве которых приняты главные сечения мульды сдвижения по простиранию и вкрест простирания пласта (рис.1). Затем определяются сдвижения и деформации по любому другому направлению, проходящему под углом к простиранию пласта. Соответствующие формулы дня расчета сдвижений и деформаций в Правилах приведены. Из анализа этих формул вытекают некоторые недостатки координатного метода расчета сдвижений и деформаций.
Calculations of displacements and deformations of the earth surface in the given points of the displacement trough with the use of polar technique
The analysis of calculations of characteristic parameters of displacements and surface deformations for conditions of mining at great depth and the method of calculations recommended by the Rules of Building Protection have a number of drawbacks. The polar technique is proposed in which the drawbacks are eliminated. The areas of its application are shown and the efficiency is noted in the conditions of flat dip.
1. Границами мульды сдвижения в этом методе являются стороны прямоугольника, равные длинам полумульд в главных сечениях (Ll2, L3).
Наклоны, например, iуl,х, в расчетной точке с координатами хуl (рис.1) определяются по формуле
где S(zx) и Ś(zyl) являются переменными величинами и выбираются из специальных таблиц Правил;
ηm - максимальное оседание в центре мульды;
Ll - длина полумульды в сторону падения (в главном сечении мульды вкрест простирания) пласта.
Величина Ll для всех сечений, параллельных главному сечению вкрест простирания, остается постоянной, следовательно, контур краевой части мульды принят прямолинейным. Такой же вывод следует из формулы для определения наклона ixyl, но в отношении длин полумульд по простиранию, которые остаются постоянными для всех сечений, параллельных главному сечению по простиранию, и равными длине полумульды в главном сечении по простиранию L3. Следовательно, граница края мульды сдвижения в расчетах принята прямоугольной, что является недостатком метода, так как граница мульды должна иметь форму эллипса.
2. Необходимым условием правильного расчета сдвижений и деформаций в промежутке между главными сечениями мульды является плавный переход от распределения сдвижении в главном сечении вкрест простирания к распределению сдвижений в главном сечении по простиранию, т.е. соблюдение граничных условий. Это условие в координатном методе не соблюдается.
 Рис. 1.
Рис. 1.
Расчет сдвижений и деформаций в заданных точках мульды сдвижения по Правилам охраны
Эти недостатки устраняются в предлагаемом нами методе расчета, который назовем полярным методом.
Полярный метод расчета сдвижений и деформаций основывается на следующих положениях и свойствах мульды сдвижения.
-
Мульда сдвижения на ее краях имеет форму эллипса. Одной полуосью эллипса является длина полумульды по простиранию L3, другой - длина нижней полумульды по падению Ll или длина полумульды по восстанию L2.
-
Мульда сдвижения имеет два главных сечения, проходящие через центр мульды точку O. Одно главное сечение - по простиранию, другое - вкрест простирания пласта (по падению и по восстанию).
Примем следующие свойства главных сечений:
-
горизонтальные сдвижения и деформации в главных сечениях происходят только в вертикальной плоскости этих сечений;
-
вертикальные и горизонтальные сдвижения и деформации земной поверхности в главных сечениях достигают максимальной величины, соответствующей данным горно-геологическим условиям;
-
функции распределений сдвижений и деформаций в главных сечениях зависят от двух параметров: коэффициентов подработки (Nl, N2 ) и параметром В, который зависит от угла падения пласта (α).
В данной работе свойства главного сечения трактуются шире, чем в Правилах охраны [1], где сказано, что главное сечения мульды проходит вкрест пристирания пласта или по простиранию через точки с максимальными оседаниями земной поверхности. Как будет показано далее, этого недостаточно для правильного применения метода расчета сдвижений и деформаций в заданных точках мульды сдвижения.
Сущность полярного метода расчета сдвижений и деформаций состоит в следующем. Рассмотрим линию ОС, проходящую через центр мульды О и расчетную точку M под углом φ к простиранию (рис.2).
 Рис. 2.
Рис. 2.
Расчет сдвижений и деформаций в заданных точках мульды сдвижения полярным способом
Считаем, что эта линия обладает всеми свойствами главных сечений, но в направлении угла φ, а именно: сдвижения и деформации по этой линии будут происходить в вертикальной плоскости, проходящей через эту линию, и будут иметь максимальную величину.
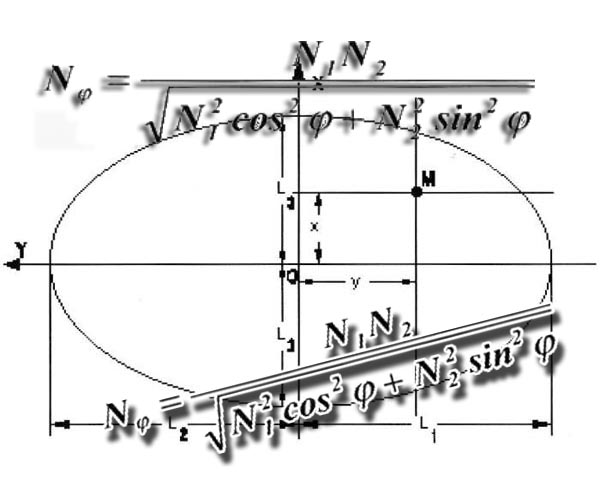
Будем исходить из следующего требования: при изменении угла φ от 0° до 90° функции распределения сдвижений и деформаций по этой линии должны плавно изменяться от их значения в главном сечении по простиранию до значения их в главном сечении вкрест простирания. Для этого надо произвести плавное интерполирование коэффициентов подработки от N2 в главном сечении по простиранию до Nl, в главном сечении вкрест простирания и плавное интерполирование углов падения α от 0° по направлению простирания до его значения по направлению вкрест простирания. Обозначим переменные значения исходных параметров через Nφ и ά. Определим сначала параметр Nφ. Интерполирование его можно произвести по линейному или тригонометрическому закону, но наиболее правильным является в данном случае интерполирование по закону эллипса
Угол падения ά интерполируется по известной формуле
Кроме параметров Nφ и ά для расчета деформаций необходимо знать длину полумульды Lφ в направлении угла φ. Полумульда изменяется от L3 в главном сечении по простиранию до Ll в главном сечении вкрест простирания (по падению пласта) и представляют собой расстояние от точки 0 до границы эллипса - границы мульды сдвижения по линии СМ. Исходя из уравнения эллипса будем иметь:
для полу мульды по падению
для полумульды по восстанию
Расчеты сдвижений и деформаций земной поверхности в направлении линии ОМ производятся по формулам Правил охраны сооружений с учетом выведенных нами интерполяционных выражений
Обозначение входящих величин в формуле (5) соответствуют Правилам охраны сооружений [1]. Векторы горизонтальных сдвижений и деформаций направлены по линии ОМ.
Следует отметить, что при угле падения более 12-15°, имеет место нарушение условий для главных сечений, оговоренных выше в данной работе. В плоскости главного сечения по по простиранию появляются существенные поперечные горизонтальные сдвижения |2]. Вертикальную поверхность по простиранию, где отсутствуют поперечные сдвиги отыскать можно, но она будет криволинейной.
Этот недостаток одинаково присущ методу изложенному в Правилах и полярному методу. Поэтому при расчете следует ограничиться пологим залеганием пластов.
Функции распределения сдвижений и деформаций в формулах (5) существенно зависят от значений параметра В. В Правилах охраны этот параметр определяется по формуле
где: α0- постоянный коэффициент равный примерно 0,3;
α- угол падения пласта;
h - мощность наносов;
Н - глубина залегания пласта.
Но формула (6) не совсем правильно отражает сглаживающую роль наносов. Из формулы следует, что чем ближе отношение h/Н к единице, т.е. когда вся толща пород состоит из наносов , а угол падения более 45°, тем больше значение параметра В, т.е. больше составляющая горизонтальных сдвижений, вызванная сдвигом пород. Тогда как при Н → h для любых углов падения горизонтальные сдвижения, вызванные сдвигом, должны стремиться к нулю.
Предлагаем формулу, которая позволяет устранить этот недостаток
Определенные по формулам (5) сдвижения и деформации в точке М являются максимальными в направлении линии расчета, во всех других направлениях они будут меньше. Но для решения вопросов защиты зданий и сооружений следует исходить именно из этих максимальных деформаций особенно при больших глубинах горных работ, когда величины максимальных деформаций соизмеримы с погрешностями их определения.
На рис. 1 приведен пример неполной подработки по простиранию и вкрест простирания N1 < 1 и N2 < 1. В этом случае полярный способ расчета может применяться для всей мульды сдвижения. Однако чаще бывает полная подработка по простиранию N2 > 1 и неполная подработка вкрест простирания N1 < 1. Тогда полярный способ расчета может применяться для краевых частей мульды.
На основании изложенного можно сделать следующие выводы.
-
В существующих правилах недостаточно полно определено понятие главного сечения мульды, а также при расчете сдвижений и деформаций на краевых участках мульды по методу прямоугольных координат границы мульды приняты в виде прямоугольника, что не соответствует действительности.
-
Рекомендуется расчет деформаций на краевых участках мульды производить полярным способом, который исключает указанные недостатки, особенно в условиях пологого залегания пластов.